
La
sphère
sans limite…

Dans le cadre de l’étude des solides en troisième secondaire, celle de la sphère en particulier ainsi que de son aire et de son volume se limite bien souvent à ne donner aux élèves que les deux formules pour qu’ils les utilisent et les appliquent dans des problèmes. Nous voulons proposer des approches différentes pour l’enseignement des concepts d’aire et de volume de la sphère. En effet, peut-on trouver des raisonnements et des représentations visuelles qui permettraient de donner un sens à ces formules et montrer une façon de les construire ? La réponse est oui et pour ce faire nous allons utiliser différentes notions et notamment celle du passage à la limite, concept rarement utilisé au secondaire, mais qui peut être introduit informellement par l’entremise de la démarche que nous proposons.
Bonne lecture,
Vincent
Scallon
Préambule :
Un des principaux
raisonnement que
nous allons utiliser fait appel à la notion de limite. Dans un
contexte donné, nous allons faire varier un paramètre de
façon qu’il tende vers une certaine limite. Par exemple,
notre paramètre va prendre des valeurs de plus en plus grandes :
il va tendre vers l'infini, ou encore il va prendre des valeurs de plus
en plus petites : il va tendre vers zéro.
En premier lieu, pour déterminer l'aire de la sphère connaissant son volume, les deux tendances vont être
exploitées. Dans un premier temps, nous allons déterminer
vers quoi tend l’aire de deux sphères (et
à la limite, d’une sphère) quand on
fait tendre la différence de leur rayon
vers zéro.
En
deuxième lieu, sachant l’aire d’une
sphère, on va déterminer
vers quoi tend le volume d’une sphère,
constituée de pyramides à base triangulaire,
quand le nombre de ces pyramides qui constituent la sphère
tend vers l’infini
et que la hauteur de
ces pyramides tend vers le rayon de la
sphère.
1- Volume de la sphère :
1.1- Le Principe
de Cavalieri (1598-1647) :
a- Calcul
d’aires :
Bonaventura
Cavalieri considérait
qu’une surface plane est composée de segments
parallèles équidistants et
indivisibles. Le théorème fondamental de sa
«méthode des indivisibles» pour les
surfaces est le suivant :
«
Si deux figures
planes du même plan (coplanaires) sont comprises entre deux
droites parallèles
et si toutes les intersections de ces deux figures avec une droite
parallèle
aux deux premières ont la même longueur, alors les
deux figures planes ont la
même aire. »
Par
exemple, pour montrer
qu’un parallélogramme
et un rectangle (ayant la même mesure de base et la
même hauteur) ont la même
aire en utilisant le théorème
précédent, nous les plaçons entre deux
droites
parallèles d1
et d2
comme illustré par la figure
ci-dessous, puis nous allons vérifier que pour toute droite
d parallèle aux
deux premières : 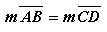
b- Calcul de volumes :
Cavalieri
concevait également un
solide comme étant constitué de surfaces planes
parallèles équidistantes et
indivisibles. Son théorème des indivisibles pour
les solides s’énonce comme
suit :
« Si deux solides sont compris entre deux plans parallèles, et si toutes les intersections de ses deux solides avec un plan parallèle aux deux premiers ont la même aire alors les deux solides ont le même volume. »
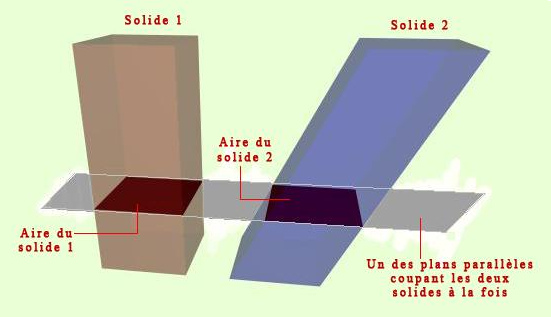
Formulation plus détaillée du principe de Cavalieri
Animation du principe de Cavalieri
Considérons une demi-sphère de rayon r reposant sur un plan horizontal P. Sur ce même plan, soit un cylindre de rayon r et de hauteur r à l'intérieur duquel on creuse un cône dont le sommet est situé au centre de la base inférieure du cylindre et dont la base est la base supérieure du cylindre tel qu’indiqué par la figure ci-dessous :

Comparons le
volume de la demi-sphère au volume du cylindre
creusé (partie du cylindre qui
n’appartient pas au cône) :
1- Nous pouvons constater que les conditions d’application du principe de Cavalieri sont vérifiées car les deux solides sont compris entre deux plans parallèles puisque le rayon de la demi-sphère est égal à la hauteur du cylindre.
2- Si on sectionne les deux solides par un plan X horizontal situé à une hauteur h, tel que 0 < h < r, nous allons obtenir dans la demi-sphère un disque et dans le cylindre creusé un anneau comme illustré par la figure ci-dessous.
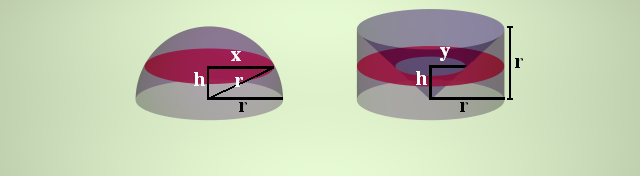
Calculons l’aire de chacune des deux intersections :
Posons x le rayon du disque qui est l’intersection du plan X et de la demi-sphère. L’aire du disque peut s’exprimer alors comme suit :
Aire
du disque = A1 = π x²
Trouvons
la valeur de x² :
En effectuant une coupe transversale sur la demi-sphère on obtient le schéma de la figure suivante :
Posons y
comme
étant le rayon du cercle intérieur.
L'aire
de l'anneau est la différence entre l'aire du cercle
de rayon r
(cercle
extérieur) et celle du cercle intérieur de rayon y.
Nous pouvons alors exprimer l'aire de l'anneau comme suit :

Cherchons la valeur de y :
Les deux triangles PCD et PEF sont rectangles respectivement en C et E. Ils ont aussi l'angle P en commun.
Par le critère AA nous pouvons dire que les deux triangles sont semblables.
Nous pouvons donc écrire :
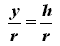
D'où :
y
= h.
Nous
pouvons alors exprimer l'aire de l'anneau comme suit :

Nous
remarquons que l'aire de l'anneau
est égale à celle du disque :

Dans
ce cas, l'intersection du
plan horizontal avec la demi-sphère est un disque de rayon r
et d'aire  .
.
L'intersection
du même plan
horizontal avec le cylindre creusé
est la base inférieure du cylindre qui est un disque de
rayon r moins le sommet
du cône qui est un point. Si nous considérons que
l'aire d'un point est nulle,
nous pouvons dire que l'aire de cette intersection est celle
du disque du rayon
r, qui est égale à  .
.
Nous pouvons dire que quand h = 0, les deux intersections ont la même aire.
Cas
où h
= r
Quand
h
= r,
le plan X
est
tangent à la demi sphère, ce qui
ramène leur intersection à un point (le point
de tangence) d'une aire nulle : A1 = 0.
L'intersection
du même plan
avec le cylindre creusé est un cercle de rayon r.
Mais comme nous
pouvons
considérer que l'aire d'un
cercle est nulle, nous pouvons en déduire que l'aire de
cette dernière
intersection est nulle : A2
=
0.
Dans ce cas aussi, les deux intersections ont la même aire.
Conclusion :
Les
sections des deux solides par les
plans horizontaux ont donc toujours la même aire, et nous en
déduisons que les
deux solides ont le même volume.
Par
conséquent le volume de la
demi-sphère équivaut à la
différence entre celui du cylindre et celui du
cône,
c'est-à-dire :
Volume de la
demi-sphère = Volume du
cylindre - Volume du cône
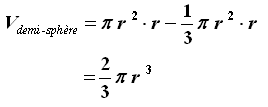
Le volume de la sphère de rayon r sera le double du volume de la demi-sphère, soit :

2-
Aire de la
sphère connaissant son volume :
Tout
d'abord,
considérons deux sphères. Soit S1 de rayon r
et S2 de rayon R et de même centre O, tel que R 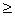 r . Posons h
= R - r (la
différence entre les
deux
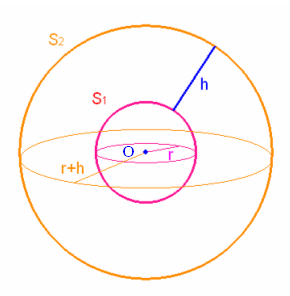
rayons). Ici, il faut insister sur le fait que la surface de la
sphère est son
«enveloppe extérieure» qui est
constituée de tous les points de l'espace
situés
à égale distance du centre O,
à ne
pas confondre avec l'aire de la sphère qui est la
mesure de sa surface.
r . Posons h
= R - r (la
différence entre les
deux
rayons). Ici, il faut insister sur le fait que la surface de la
sphère est son
«enveloppe extérieure» qui est
constituée de tous les points de l'espace
situés
à égale distance du centre O,
à ne
pas confondre avec l'aire de la sphère qui est la
mesure de sa surface.
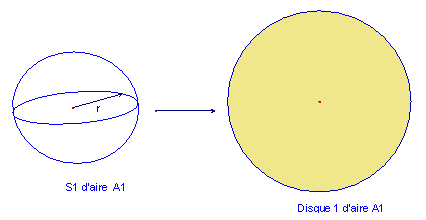
1- Nous avons
associé à chaque sphère (objet en
trois dimensions) une figure plane ayant la même aire (objet
en deux dimensions).
La nature de la figure plane associée à chaque sphère n'a aucune influence sur le raisonnement qui suit, mais pour simplifier les représentations nous avons opté pour le disque sachant que c'est faisable (et que c'est une très bonne idée!).

2- Nous allons
construire trois nouveaux solides :
A- Un cylindre
droit C1
dont la base a la
même aire A1
que la
sphère S1
(disque 1) et
dont la hauteur est égale à h
(la différence entre les rayons des deux sphères
: h
= R
- r).
Soit V1
son
volume (il faut noter que le volume de ce
cylindre n'est pas le même que celui de la
sphère S1).
Cylindre
C1 :
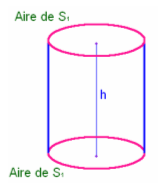
B- Un cylindre droit C2 dont la base a la même aire A2 que la sphère S2 et dont la hauteur est aussi h.
Soit V2 son volume (il faut aussi noter que le volume de ce cylindre n'est pas le même que celui de la sphère S2).
Cylindre C2 :

- la
petite
base a une aire de A1
(la
même aire que la sphère S1)
- la
grande
base a une aire de A2
(la
même aire que la sphère S2)
- la
hauteur
est égale à h
Soit V3 son volume.
Tronc de cône T1 :
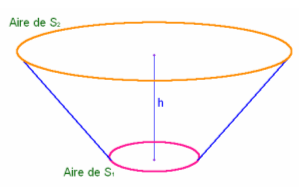
3- Maintenant
que nous avons construit ces trois solides, on va mettre leurs volumes
en relation.
Nous
savons que :
- le volume
d'un cylindre dépend de la hauteur et de
l'aire de la base.
- le volume d'un tronc de cône dépend de la hauteur et de l'aire de ses deux bases.
Mais
comme les trois solides ont la même
hauteur,
leurs volumes dépendent uniquement des aires de leurs bases.
Nous pouvons
admettre que l'aire de S1
est toujours inférieure ou égale à
l'aire de S2, puisque
nous
avons posé 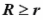
(la
sphère S1
est soit à
l'intérieur de la sphère S2 quand
r <
R, soit confondue avec cette
dernière lorsque r =
R).
Nous pouvons établir les
inégalités
suivantes entre les trois volumes en question
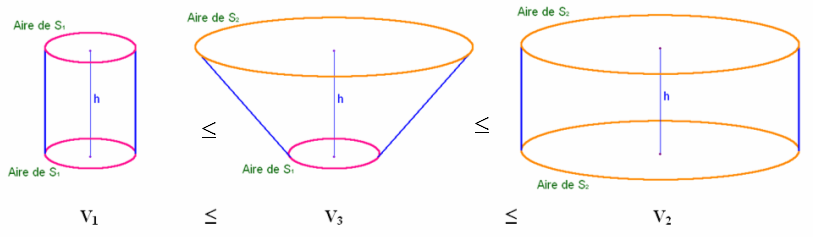
Autre représentation des solides imbriqués les uns dans les autres
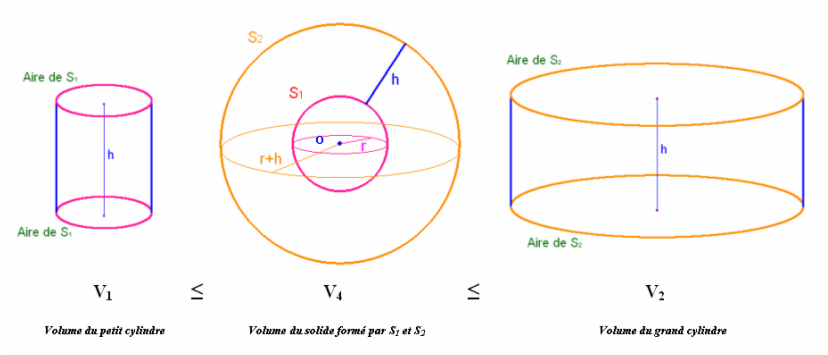
Il faut noter
qu'en
réalité, le volume du tronc de cône est
égal au volume du solide ayant pour
parois les deux sphères S1 et S2,
même si ce
n'est pas indispensable pour notre démarche.
Volume de T =
V3 = V4= Volume de S2 -
Volume de S1 (voir annexe)
Calculons
maintenant
les volumes V1,
V2
et V4, sachant que R = r + h :
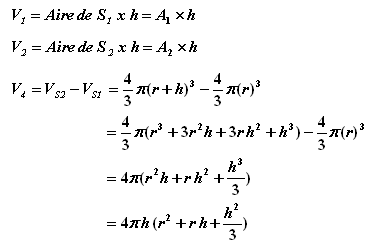
En remplaçant chacun des volumes par son expression dans la double inégalité précédente nous allons obtenir :
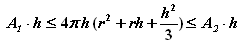
En divisant
chacun des termes par h, nous
allons obtenir

Maintenant,
observons
qu'est-ce qui va arriver si la valeur de h
diminue, autrement dit
si la distance entre les deux sphères diminue ?

Animation alternative (de côté et du dessus)
Le volume de
la
sphère S1,
de même que son aire, vont se rapprocher de
ceux de la sphère S2.
Et que
va-t-il
arriver, à la limite? Quand h
va devenir très
petit (qu'il va tendre vers zéro)?
Les termes r
h et  vont
devenir aussi très petit (ils vont tendre vers zéro) et
à la limite, vont être égal à zéro
quand h va égaler zéro.
vont
devenir aussi très petit (ils vont tendre vers zéro) et
à la limite, vont être égal à zéro
quand h va égaler zéro.
Ainsi, notre double inéquation deviendra :
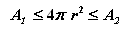
C'est-à-dire que
quand h tend vers
zéro, les deux
sphères se confondent et l'aire de la
sphère S1 égale l'aire de la
sphère S2 qui égale  , ce qui
est bien l'aire d'une sphère de rayon r.
, ce qui
est bien l'aire d'une sphère de rayon r.
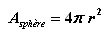 .
.
Supposons maintenant que nous
connaissons
la formule pour exprimer l'aire d'une
sphère, soit : 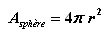 . Pouvons-nous trouver
l'expression de son volume?
. Pouvons-nous trouver
l'expression de son volume?
Commençons par une approximation de la sphère et construisons un solide constitué de n pyramides à bases triangulaires.
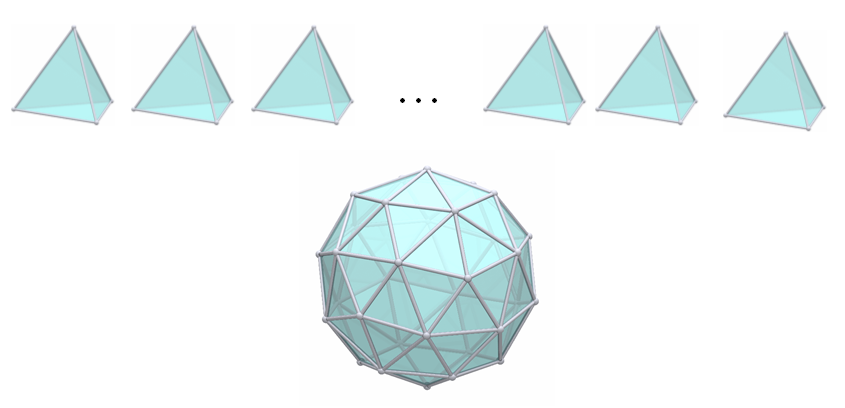
Le volume du solide obtenu est égal à la somme des volumes des n pyramides à bases triangulaires qui le composent.
Le
volume d'une
pyramide dépend de
l'aire de sa base et de
sa hauteur :
Volume
d'une
pyramide = 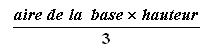

Nous remarquons que plus le nombre de pyramides augmente, plus notre solide se rapproche de la sphère. En fait, lorsque leur nombre tend vers l'infini, la somme des aires des bases des pyramides tend vers l'aire de la sphère et la hauteur des pyramides tend vers le rayon de la sphère. À la limite, quand il va y avoir une infinité de pyramides, la hauteur des pyramides va être égale au rayon.

Ainsi, pour un solide constitué d'un très grand nombre de pyramides, nous pouvons considérer que :

D'où le volume de la sphère :

Et à la limite quand h = r :

À partir de la formule de l'aire de la sphère, nous avons retrouvé par approximation la formule de son volume.
Nous savons que le volume d'une sphère est donné par :

Et celui d'un cône par :
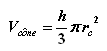
Pour un cône ayant une hauteur égale au rayon de la sphère ainsi que le même volume que celle-ci,
i.e.  et
et
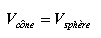 :
:


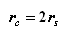 :
Le rayon
de la base du cône est deux fois plus grand que celui de la
sphère.
:
Le rayon
de la base du cône est deux fois plus grand que celui de la
sphère.

nous arrivons aisément à la conclusion que le solide ayant les deux sphères comme parois et le tronc de cône T ont le même volume.